Cost function!
If you have data of any task X and its desire output Y and if you are able to form a cost function then you can get desired behaviour from neural network.
The procedure repeatedly adjusts the weights of the connections in the network so as to minimize a measure of the difference between the actual output vector of the net and the desired output vector.[1]
How do we measure difference between actual output of neural net and desired output? Using the cost function. Let's see what it means by one example.
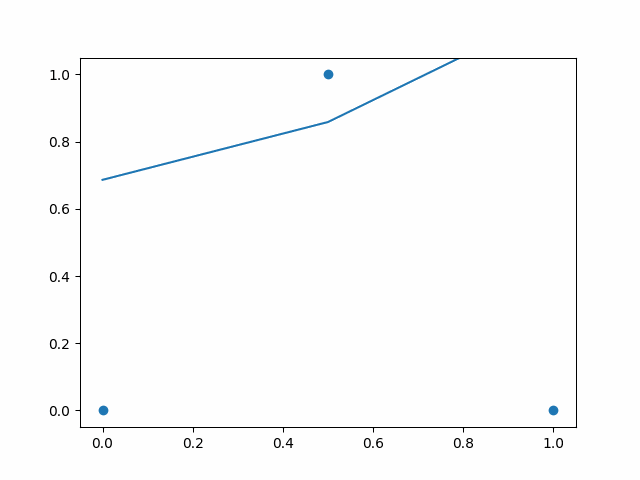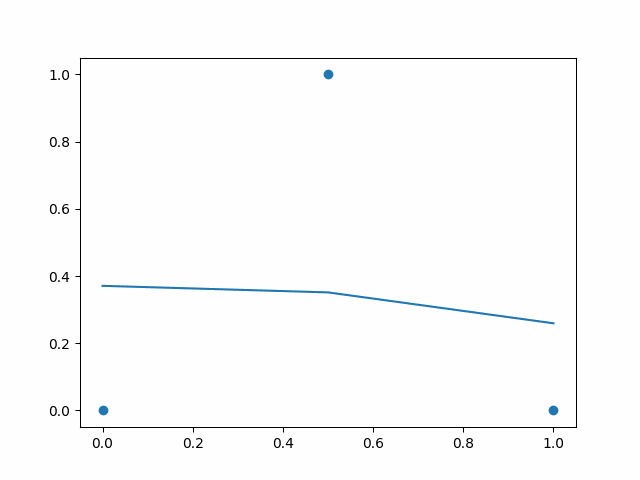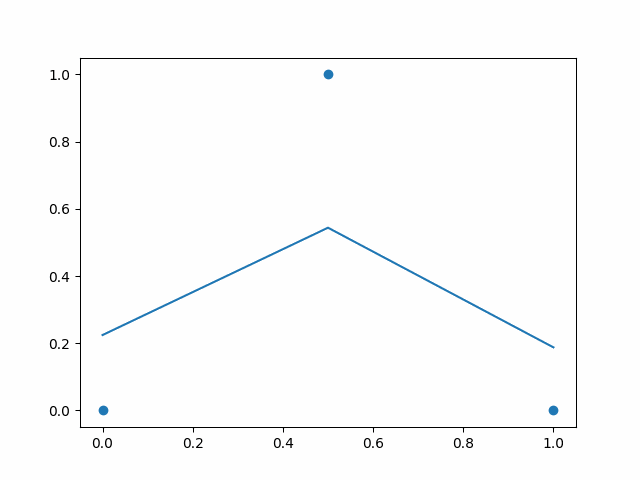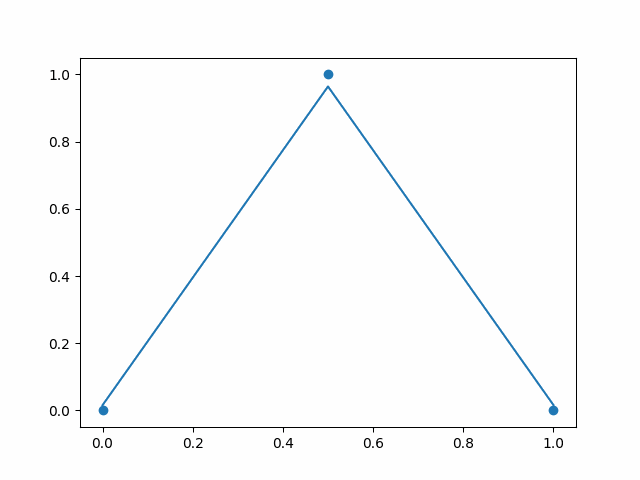
For above example I have used simple three point dataset where we give input between 0 to 1 on x-axis. Values near to 0 and 1 gives output as near to 0, and input in the middle like 0.5 gives output as near to 1. In above example I have shown output of neural network over the time. As you can see, initially the line is flat and does not touch the data points. Over the time line bends and tries to touch the data points. So the initial stat is before training neural net — where predicted values by network is far from desired values. And after the training it pridicts the output that is desired.
To calculate error I define a function \(E\) that will measure difference of output predicted by neural network and desired values. High error means neural net predicted values that are far from desired values, and low means it is nearer to desired values.
Now look at this picture.
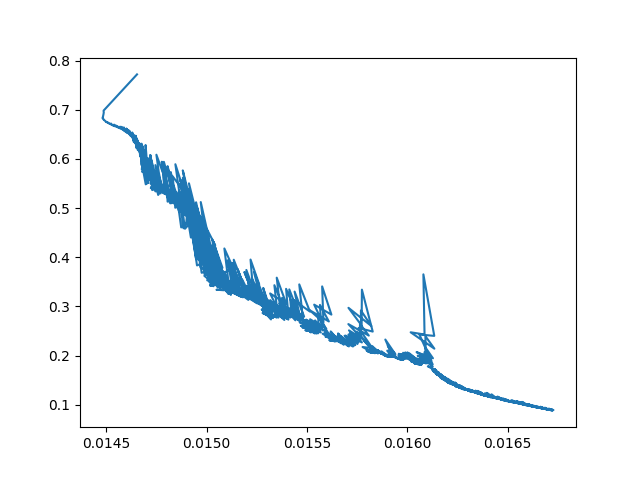
Here x-axis is different values of one of the weight \(w\) of one of the layer of the neural net. And y-axis is the loss value or error for different values of weight. And this picture shows that neural network figured out a value for weight that gives a lowest error — meaning predicted value is near to desired value that we calculated using cost function.
But the question is how NN updated its weight value?
To minimize E by gradient descent it is necessary to compute the partial derivative of E with respect to each weight in the network. This is simply the sum of the partial derivatives for each of the input-output cases. For a given case, the partial detivatives of the error with respect to each weight are computed in two passes. We have already described the forward pass in which the units in each layer have their states determined by the input they receive from units in lower layers using equations (1) and (2). The backward pass which propagates derivatives from the top layer back to the bottom one is more complicated. [1]
Taking partial derivative of error with respect to all the weights of the network. What does the partial derivative will tell us?
This means that we know how a change in the total input x to an output unit will affect the error.[1]
It's rise over run — if we nudge weights current value by small value how much impact will it have on value of error. We will keep updating the weights till we get low error.
So the takeaway is that if we are able define a cost function that gives high value when network predicts values far from desired values and vice versa we can train model to perform any task.
For example for in query focued video summarization loss function is binary cross entropy that is for binary classification — weather or not shot is relevent to query or not(1 or 0). But here we also want diverse clips from long video, and for that Narasimhan et. al. in CLIP-it[2] proposed Diversity loss along with classification loss.
So it looks like we can change behavior of neural network by defining a cost function.
Try Yourself Here is the binary classification loss equation and its code. Our desired output is only two {0, 1} so pass y as 0 and yh as its oposite that is 1 and you should get a high value. and now pass y as 0 and yh as near to 0 eg. 0.003, you will get low value.
# y - Actual class
# yh - Model prediction
def cost(y, yh):
return -((y*math.log(yh)) + ((1-y)*math.log(1-yh)))
References
[1] Learning representations by back-propagating errors, David E. Rumelhart, Geoffrey E. Hintont & Ronald J. Williams, 1986.
[2] CLIP-It! Language-Guided Video Summarization, Medhini Narasimhan, Anna Rohrbach, and Trevor Darrell, 2021